Today, I will talk to you about some techniques that are commonly used when doing algorithm problems. For those who haven't used these techniques before, maybe you can consider trying to see if you can use these techniques in practice to optimize the solution of the problem.
1. Clever use of array subscripts
The subscript of an array is an implicitly useful array, especially when counting some numbers, or judging whether some integer numbers have appeared. For example, when we give you a string of letters and let you judge the number of occurrences of these letters, we can use these letters as subscripts. When traversing, if the letter a is traversed, then arr[a] can be increased by 1, i.e. arr[a]++;
Through this clever use of subscripts, we don't need to judge letter by letter.
I'll give another example:
Question: You are given n unordered int integer arrays arr, and the value range of these integers is between 0-20. In the time complexity of O(n), you need to arrange these n numbers from small to small Large order prints out.
For this question, if you sort the n numbers first, and then print them, it is impossible to print them out in O(n) time. But the value range is 0-20. We can use array subscripts cleverly. The corresponding value is used as the subscript of the array. If this number appears, the corresponding array is incremented by 1.
code show as below:
public void f(int arr[]) { int[] temp = new int[21]; for (int i = 0; i
Reminder: You can swipe left and right
There are still many applications of using array subscripts. When you encounter some problems in the future, you can consider whether you can use array subscripts to optimize.
2. Use the remainder wisely
Sometimes when we traverse the array, we will make out-of-bounds judgment. If the subscript is almost out of bounds, we will set it to 0 and re-traverse. Especially in some circular arrays, such as queues implemented with arrays. Code like this is often written:
for (int i = 0; i
We can actually simplify the code by taking the remainder
for (int i = 0; i
3. Use double pointers skillfully
For double pointers, it is especially useful for questions about singly linked lists, such as "judging whether a singly linked list has a cycle", "how to find the node in the middle of the linked list in one traversal", "the last kth node in a singly linked list" and other questions. For this kind of problem, we can use double pointers, which will be much more convenient. By the way, let me explain how to solve these three problems with double pointers.
For example for the first question
We can set a slow pointer and a fast pointer to traverse the linked list. The slow pointer moves one node at a time, while the fast pointer moves two nodes at a time. If the linked list does not have a ring, the fast pointer will traverse the list first. If there is a ring, the fast pointer will meet the slow pointer in the second traversal. .
for the second question
The same is to set a fast pointer and a slow pointer. The slow moves one node at a time, and the fast two. When traversing the linked list, when the fast pointer traversal is complete, the slow pointer just hits the midpoint.
for the third question
Set two pointers, one of which moves k nodes first. Both hands then move at the same speed. When the traversal of the first moved pointer is complete, the second pointer is exactly at the k-th node from the bottom.
You see, it is much more convenient to use double pointers. So in the future, when dealing with some problems related to linked lists, you can consider double pointers.
4. Use shift operations skillfully.
Sometimes when we perform divisor or multiplier operations, such as n / 2, n / 4, n / 8, we can use the shift method to operate, which will be much faster.
For example:
n / 2 is equivalent to n >> 1
n / 4 is equivalent to n >> 2
n / 8 is equivalent to n >> 3.
In this way, the execution speed of the shift operation will be faster, and it can also show that you are very powerful, haha.
There are also some & (and), | (or) operations, which can also speed up the operation. For example, to determine whether a number is odd, you might do
if(n % 2 == 1){ dosomething();}
But it would be much faster if we used AND-OR. For example, to determine whether it is an odd number, we can add n and 1. If the result is 1, it is an odd number, otherwise it is not. which is
if(n & 1 == 1){ dosomething();)
For some specific computing skills, you still need to try to use them in practice, so that you will become more proficient after using them for a long time.
5. Set the sentinel bit
In the related problems of linked list, we often set a head pointer, and this head pointer does not store any valid data, just for the convenience of operation, we can call this head pointer a sentinel bit.
For example, if we want to delete the first node when the head first, if a sentinel bit is not set, then in operation, it will be different from the operation of deleting the second node. But we set a sentinel, then deleting the first node and deleting the second node are the same in operation, and no additional judgment is required. Of course, the same is true when inserting nodes.
Sometimes when we operate an array, we can also set a sentinel, and use arr[0] as the sentinel. For example, when judging whether two adjacent elements are equal, setting a sentinel is not afraid of out of bounds and other problems, you can directly arr[i] == arr[i-1]?. Don't be afraid of out of bounds when i = 0.
Of course, this is just an example, there are many specific applications, such as insertion sort, circular linked list, etc.
6. Some optimizations related to recursion
(1). Consider state preservation for recursive problems
When we use recursion to solve a problem, it is easy to repeatedly calculate the same sub-problem. At this time, we need to consider state preservation to prevent repeated calculation. For example, let me take a random question that I raised before
Question: A frog can jump up 1 steps at a time, or 2 steps at a time. How many ways can the frog jump up a n steps?
This problem is easily solved with recursion. Assuming that f(n) represents the total number of hops of n steps, there are
f(n) = f(n-1) + f(n - 2).
The end condition of the recursion is when 0
public int f(int n) { if (n
However, for problems that can be solved using recursion, we must consider whether there are many repeated calculations. Obviously for the recursion of f(n) = f(n-1) + f(n-2), there are many repeated calculations. like
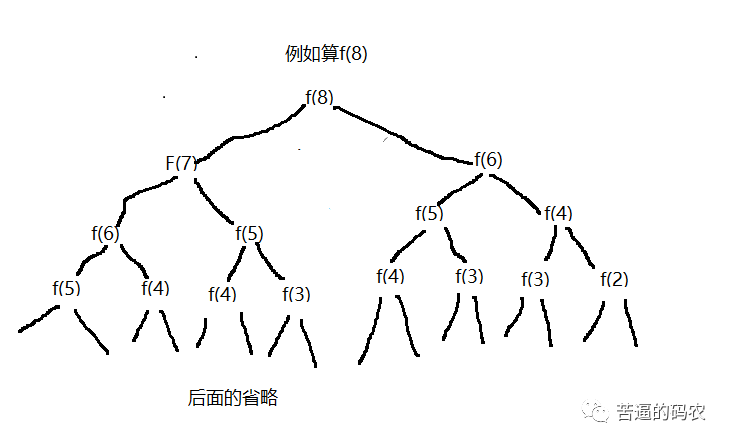
There is a lot of double counting. This time we have to consider state preservation. For example, using hashMap to save, of course, it is also possible to use an array. At this time, as we said above, we can use array subscripts skillfully. When arr[n] = 0, it means that n has not been calculated. When arr[n] != 0, it means that f(n) has been calculated. At this time, the calculated value can be returned directly. Therefore, the code we consider to save the state is as follows:
//The size of the array depends on the specific situation, because the default value of the int array element is 0 //So we don't need to initialize int[] arr = new int[1000]; public int f(int n) { if (n
In this way, the efficiency of the algorithm can be greatly improved. Some people also call this state preservation the memorandum method.
(2). Consider bottom-up
For recursive problems, we generally recurse from top to bottom until the recursion reaches the bottom, and then return the value layer by layer.
However, sometimes when n is relatively large, such as when n = 10000, then it is necessary to recurse down 10000 levels until n
In this case, we can actually consider a bottom-up approach. For example I know
f(1) = 1;
f(2) = 2;
Then we can deduce that f(3) = f(2) + f(1) = 3. Thus it can be deduced that f(4), f(5), etc. up to f(n). Therefore, we can consider using a bottom-up approach to do it.
code show as below:
public int f(int n) { if(n
We also call this bottom-up approach recursion.
in conclusion
When you are using recursion to solve problems, consider the following two problems
(1). Whether there is state repeated calculation, can you use the memorandum method to optimize.
(2). Whether the recursive method can be used from the bottom up to reduce the overhead of blind recursion.
I'll stop here today, and I'll thank you for some others later when I have time. If you think it's good, please give it a thumbs up.
Liquid Crystal Display For Instrument
Liquid Crystal Display For Instrument,Large Industrial Precision Lcd Display,Small Industrial Body Thin Lcd Display,Precise Liquid Crystal Display
Dongguan Yijia Optoelectronics Co., Ltd. , https://www.everbestlcdlcms.com