Based on NumPy to build neural network from scratch, step by step explained in detail

Editor's Note: Together with Daphne Cornelisse based on NumPy to build a neural network from scratch, including a detailed step-by-step explanation, and in this process introduce the basic concepts of neural networks.

This article will describe the steps required to create a three-layer neural network. I will explain this process while you are solving the problem, while introducing some of the most important concepts.

Need to solve the problem

A farmer's labelling machine in Italy failed: The labels of three different varieties of wine were mixed. With 178 bottles left, no one knows what kind of wine each bottle is! To help this poor person, we will create a classifier that identifies the breed based on the 13 attributes of the wine.

Our fact that our data is tagged (one of three species) means that we face a supervised learning problem. Basically, what we want to do is use our input data (178 bottles of unclassified wine), through the neural network, to output the correct label for each bottle of wine.

We will train the algorithm to make it more powerful to predict which label each bottle belongs to.

It is time to start creating neural networks!

method

Creating a neural network is like writing a very complicated function or cooking a very difficult dish. At first, the ingredients and steps you need to consider look scary. However, if you break everything down, step by step, it will be very smooth.

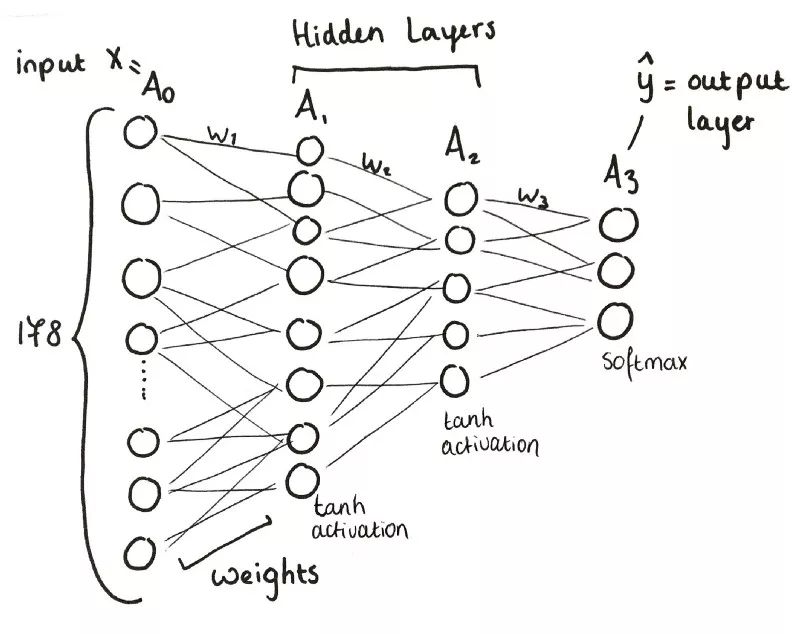
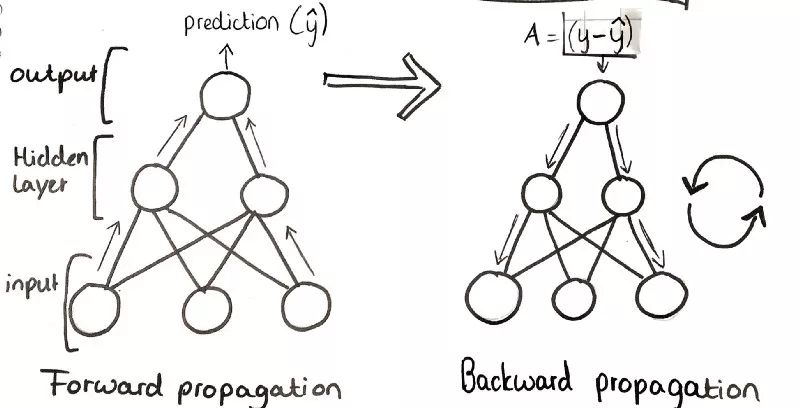
Three-layer neural network overview

simply put:

The input layer (x) contains 178 neurons.

A1, the first layer, contains 8 neurons.

A2, the second layer, contains 5 neurons.

A3, the third layer, also the output layer, contains 3 neurons.

The first step: preparation

Import all required libraries (NumPy, scikit-learn, pandas) and datasets, define x and y.

# Import libraries and data sets

Import pandas as pd

Import numpy as np

Df = pd.read_csv('../input/W1data.csv')

Df.head()

# Matplotlib is a painting gallery

Import matplotlib

Import matplotlib.pyplot as plt

# scikit-learn is a library of machine learning tools

Import sklearn

Import sklearn.datasets

Import sklearn.linear_model

From sklearn.preprocessing importOneHotEncoder

From sklearn.metrics import accuracy_score

The second step: initialization

Before using weights, we need to initialize the weights. Since we do not currently have a value for the weight, we use a random value between 0 and 1.

In Python, the random.seed function generates "random numbers." However, random numbers are not really random. These generated numbers are pseudo-random, meaning that they are generated by very complex formulas that look random. To generate a number, the formula needs the previously generated value as input. If no numbers have been generated before, the formula often accepts time as input.

So here we set a seed for the generator - make sure we always get the same random number. We provide a fixed value where we choose zero.

Np.random.seed(0)

Step 3: Forward propagation

Training a neural network can roughly be divided into two parts. First, it propagates forward through the network. That is, forward "step" and compare the result with the real value.

After using the pseudo-random number to initialize the weights, we perform a linear forward step. We add a bias to the dot product of input A0 and randomly initialized weights. At the beginning, our bias value is 0.

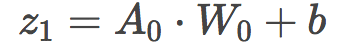
Then we pass z1 (linear step) to the first activation function. The activation function is a very important part of the neural network. By converting a linear input to a nonlinear output, the activation function introduces a non-linear function to our function, allowing it to represent more complex functions.

There are many different kinds of activation functions (this article describes them in detail). In this model, we choose the tanh activation function for two hidden layers, A1 and A2, whose output range is -1 to 1.

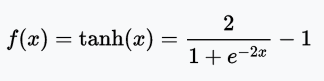
Since this is a multi-class classification problem (we have 3 output tags), we will use the softmax function in the output layer A3, which will calculate the probability of classification, that is, the probability that each bottle of wine belongs to 3 categories, and ensure that 3 The sum of the probabilities is 1.

Let z1 pass the activation function, we create the first hidden layer - A1 - the output value can be used as the input to the next linear step z2.

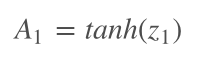
In Python, this step looks like this:

# Forward propagation function

Def forward_prop(model,a0):

# Load model parameters

W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'], model['W3'], model[' B3']

# First linear step

Z1 = a0.dot(W1) + b1

# Let it pass the first activation function

A1 = np.tanh(z1)

# The second linear step

Z2 = a1.dot(W2) + b2

# Let it pass the second activation function

A2 = np.tanh(z2)

# The third linear step

Z3 = a2.dot(W3) + b3

# The third activation function uses softmax

A3 = softmax(z3)

# Save all calculated values

Cache = {'a0':a0,'z1':z1,'a1':a1,'z2':z2,'a2':a2,'a3':a3,'z3':z3}

Return cache

Step 4: Backward propagation

After propagating forward, we propagate the error gradient back to update the weight parameters.

We inversely propagate the derivative of the network weight (W) by calculating the error function, that is, the gradient fall.

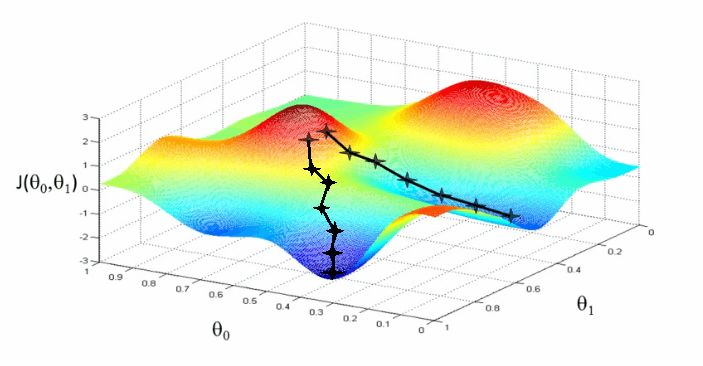
Let us visualize this process through an analogy.

Imagine you walk to the mountains in the afternoon. After an hour, you are a bit hungry. It's time to go home. The only problem is that the sky is getting dark and there are still many trees in the mountains. You can't see where your home is and you can't figure out where you are. Hey, you forgot your phone at home.

However, you still remember your house in the valley, the lowest point of the entire area. So, if you go down the mountain step by step, until you do not feel any slope, you are theoretically home.

So you walk down carefully, step by step. Now imagine the mountain as a loss function and think of you as an algorithm trying to find the home (ie, the lowest point). Every time you step down, we update your position coordinates (the algorithm updates its parameters).

Hill represents the loss function. To get lower losses, the algorithm decreases along the slope of the loss function—that is, the derivative.

As we walk down the mountain, we update the coordinates of the location. The algorithm updates the neural network weights. By approaching the minimum, we approach our goal - minimizing errors.

In reality, the gradient drop looks like this:

We always start by calculating the slope of the loss function (relative to the linear step z).

We use the following notation: dv is the derivative of the loss function to the variable v.

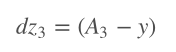
Then we calculate the slope of the loss function with respect to weights and offsets. Since this is a 3-layer neural network, we will iterate this process on z3,2,1,W3,2,1,b3,2,1. Reversely propagates from the output layer to the input layer.

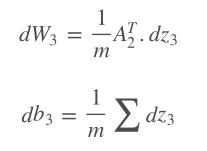
In Python, this process is this:

# This is the inverse propagation function

Def backward_prop(model,cache,y):

# Load parameters from the model

W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'], model['W3'], model[' B3']

# Load forward propagation results

A0,a1,a2,a3 = cache['a0'],cache['a1'],cache['a2'],cache['a3']

# Get the number of samples

m = y.shape[0]

# Calculate the derivative of the loss function to the output

Dz3 = loss_derivative(y=y,y_hat=a3)

# Calculate the derivative of the loss function to the second layer weight

dW3 = 1/m*(a2.T).dot(dz3)

# Calculate the derivative of the loss function to the second layer offset

Db3 = 1/m*np.sum(dz3, axis=0)

# Calculate the derivative of the loss function to the first layer

Dz2 = np.multiply(dz3.dot(W3.T) , tanh_derivative(a2))

# Calculate the derivative of the loss function to the first layer weight

dW2 = 1/m*np.dot(a1.T, dz2)

# Calculate the derivative of the loss function to the first level offset

Db2 = 1/m*np.sum(dz2, axis=0)

Dz1 = np.multiply(dz2.dot(W2.T), tanh_derivative(a1))

dW1 = 1/m*np.dot(a0.T,dz1)

Db1 = 1/m*np.sum(dz1,axis=0)

# Save gradient

Grads = {'dW3':dW3, 'db3':db3, 'dW2':dW2,'db2':db2,'dW1':dW1,'db1':db1}

Return grads

Step 5: Training Phase

In order to achieve the best weights and biases that can give us the desired output (three wine varieties), we need to train our neural network.

I think this is very intuitive. Almost everything in life, you need to train and practice many times before you can be good at it. Similarly, neural networks need to go through many epochs or iterations to give accurate predictions.

When you learn anything, like reading a book, you have a specific rhythm. The rhythm should not be too slow, or it will take years to finish reading a book. But the rhythm can't be too fast, otherwise you may miss the very important content in the book.

In the same way, you need to specify a "learning rate" for the model. The learning rate is the coefficient multiplied when the parameter is updated. It determines how fast the parameters change. If the learning rate is low, training will take more time. However, if the learning rate is too high, we may miss the minimum.

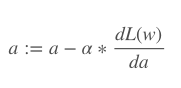
:= means that this is a definition, not an equation, or a proof of conclusion.

a is the learning rate (called alpha).

dL(w) is the derivative of the total loss to the weight w.

Da is the derivative of alpha.

We set the learning rate to 0.07 after some trials.

# This is what we finally returned

Model = initialise_parameters(nn_input_dim=13, nn_hdim= 5, nn_output_dim= 3)

Model = train(model,X,y,learning_rate=0.07,epochs=4500,print_loss=True)

Plt.plot(losses)

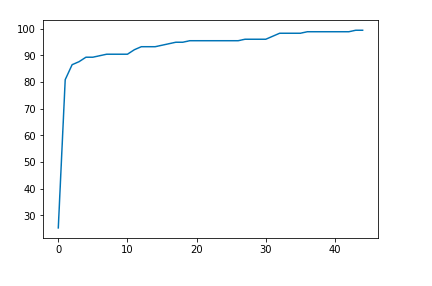
In the end, this is our image. You can plot the accuracy and/or loss to get an image of the predicted performance. After 4500 epochs, our algorithm achieved 99.4382022472% accuracy.

Short summary

We start by feeding data into a neural network and performing some matrix operations on the input data layer by layer. At each of the three network layers, we add offsets to the dot product of the inputs and weights, and then pass the output to the selected activation function.

The output of the activation function then acts as the input to the next layer and repeats the previous process. This process iterates three times because we have three network layers. Our final output is the prediction of which wine belongs to which breed, which is the end point of the forward propagation process.

We then calculate the difference between the predicted and expected output and use this error in the back propagation process.

In the back propagation process, we propagate the error in the opposite direction on the network through some mathematical method. We learn from mistakes.

By calculating the derivative of the function we use in the forward propagation process, we try to find out what weight we should give to make the best possible prediction. Basically, we want to know the relationship between the weight value and the error of our results.

After many epochs or iterations, neural network parameters gradually adapt to our data set, learning to give more accurate predictions.

This article is based on the challenge of the first week of the Bletchley Machine Learning Camp. In this training camp, we discuss a different topic each week and complete a challenge (need to really understand the material for discussion).

MT3-Normal Size Dustproof Micro Switch

Features

â—† Designed For Water and Dust Tight(IP67)

â—† Customized Designs

Normal Size Dustproof Micro Switch,Normally Open Micro Switch,Normally Closed Micro Switch,Momentary Dust Proof Switch

Ningbo Jialin Electronics Co.,Ltd , https://www.donghai-switch.com