In recent years, permanent magnet synchronous motors (PMSMs) have been widely used in servo systems due to their advantages such as high torque and current ratio and high efficiency. With the increase in demand for quick positioning and simple debugging, higher requirements are placed on the servo drive control technology. Therefore, the servo system control technology composed of PMSM has become a research hotspot. For the disturbance of the load torque disturbance and parameter perturbation in the permanent magnet synchronous motor system, people adopt different ideas to solve. On the one hand, based on classical PID control, the online adjustment of parameters is studied. On the other hand, advanced control theories such as intelligent control technology, sliding mode variable structure control, predictive control, and observer have also been extensively studied.
This paper proposes a dual-loop control method based on auto-disturbance rejection control for PMSM position control. The ADRC is introduced into the control of the PMSM servo system. The second-order non-linear ADRC is used to realize the combined control of position and speed. From the control structure, the traditional position, speed, and current three-loop cascade control are converted into position current double-loop control, which simplifies Servo system debugging process and improve the dynamic response speed. Based on the mathematical model of the servo system, the design method of second-order nonlinear ADRC and first-order linear ADRC of the current loop is given. The dynamic response and anti-disturbance performance of the servo system are also studied.
First, ADRC anti-jamming mechanismThe key to the ADRC's ability to improve the system's anti-jamming capability is to extract the interference signal from the controlled output and perform disturbance compensation in the control law. In order to observe disturbances in the system, an extended state observer needs to be designed, which tracks the estimated state variables and disturbance quantities of the system with the actual output y and the control u, as follows:

Where: z1, z2,..., Zn are observed values ​​of the state variable; zn+1 is the disturbance estimate; β01, β02,..., β0 (n+1) are observer parameters.
When φi(e) is a linear function, ESO is a linear observer, and when φi(e) has a nonlinear characteristic, it is a nonlinear observer. The state variables and disturbance values ​​of the system are accurately estimated by appropriately selecting the parameter β.
Second, servo system auto disturbance rejection control1, servo system disturbance analysis
In the synchronous rotating coordinate system, the electromagnetic torque Te can be expressed as
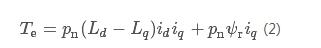
Where: pn is the number of pole pairs of the motor; iq and id are the currents of the straight axis; Lq and Ld are the inductances of the straight shaft; ψr is the rotor flux. The equation of motion is
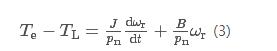
Where: TL is the load torque; ωr is the electrical angle speed; J is the moment of inertia; B is the coefficient of viscous friction.
In surface-mounted synchronous motors with Ld=Lq, combined with (2) and (3), a second-order system with electrical angle θ and rotor electrical angle speed ωr as variables can be established:
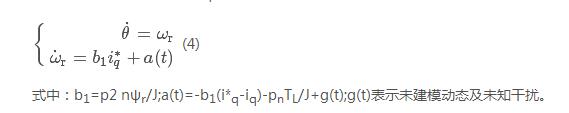
For the second-order system with iq as input and the electrical angle θ as the output, a(t) can be regarded as the total disturbance of the position control loop, including the q-axis current loop control error, load torque, rotor flux linkage, moment of inertia and other parameters Changes, unmodeled dynamics represented by g(t), etc.
When a disturbance occurs, the traditional feedback control method that depends on the error will only adjust after the position or velocity deviation occurs, and there must be a certain degree of lag. In order to achieve high-performance control, it is necessary to quickly suppress the influence of these disturbances on the position control. In this paper, the disturbance of the system is estimated and compensated by the auto-disturbance rejection controller to improve the system's immunity to disturbances.
2, displacement planning
The servo system's dynamic response is too fast and may cause overshoot in positioning. In order to suppress the overshoot in the process of position tracking, this paper adopts a tracking differentiator composed of discrete speed control synthesis function fhan to perform the displacement planning. The expression of the synthesis function fhan is as follows:
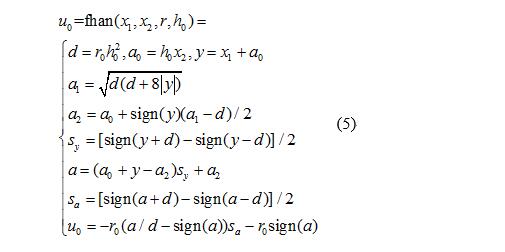
Where: x1 and x2 are input variables; r and h0 are adjustment parameters; u0 is a function output value; other are intermediate variables.
Therefore, the displacement plan is shown in Equation (6). The parameter h0 is taken as the operation cycle of the displacement plan. The speed of the position command tracking is adjusted by the unique parameter r0. This displacement planning method can not only track a given position command but also have an inhibitory effect on the noise therein.

Where: θref is the given position; θ*(k) and ω*r(k) are the actual position and velocity commands for the k-th operation cycle in the position tracking process, respectively, k ≥ 0, and there is θ at steady state. *=θref; h is the displacement planning calculation period; r0 determines the tracking speed.
3. Position and speed compound control based on auto-disturbance rejection
To realize ADRC, we need to observe disturbances in the system. In combination with (4), we use the electrical angle θ of the PMSM and the given value i* q of the q-axis current to dynamically estimate the position and disturbance of the servo system. The third-order extended state observer It can be expressed as

Where θ^(k)θ^(k) and ω^r(k)ω^r(k) are the electrical angles of the kth operation cycle, respectively
Degree θ and the estimated value of the electrical angular velocity ωr, k ≥ 0; e is the observation error; fal is a nonlinear function; z1 is the observed value of the perturbation quantity; β01, β02, β03 are the observer coefficients; h1 is the position loop control period.
among them,
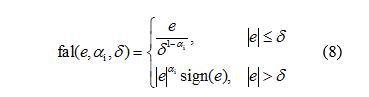
Where: δ is the error threshold; sign is a sign function; αi is a parameter.
The fal function has the characteristics of "large error, small gain; small error, large gain"; δ represents a linear interval, the purpose is to avoid high-frequency chatter caused by high gain when the error is small.
The block diagram of implementation of the nonlinear third-order extended state observer is shown in the position ESO of Fig. 2. The disturbance z1 of the position loop is estimated in real time through the position information θ, such as load torque change, system inertia change, etc., and disturbance feedforward Ways to compensate to the system, improve the system's interference suppression capabilities.
In order to make the position loop have higher disturbance rejection adjustment efficiency, the error feedback law adopts the nonlinear control law of the following formula (9), including position error, feedback path of velocity error, and feedforward channel of perturbation z1. A loop is used to realize the combined control of position and speed. When the position loop is designed, it is not limited by the bandwidth of the speed loop, which not only simplifies the control structure but also facilitates the tuning of the system parameters.
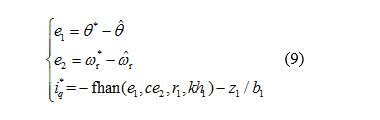
Where: b1 = p2 nψr/J; c, r1, and k are control parameters; h1 is the position loop control period; fhan function is described in Equation (5).
The parameter r1 is the control gain. When the system error is large, the value of r1 is appropriately increased, and the error tends to zero. The parameter c is introduced before the speed error to adjust the speed control effect in the compound control. Figure 1 shows the contour of the fhan function for r = 3.5, h1 = 0.001, k = 1000, c for 1 and 6, respectively. It can be seen that as the parameter c increases, the linear adjustment region of the output of the fhan function decreases, increasing the effect on the speed control. However, this does not mean that the larger the values ​​of r1 and c are, the better, because excessive control gain may cause high-frequency chattering in the steady state. In this case, the value of k must be increased appropriately.

Figure 1 The contour of the fhan function at r=3.5, different c values
Therefore, the block diagram of the position and speed control based on nonlinear auto-disturbance rejection is shown in Figure 2. The given position θref passes the displacement gauge
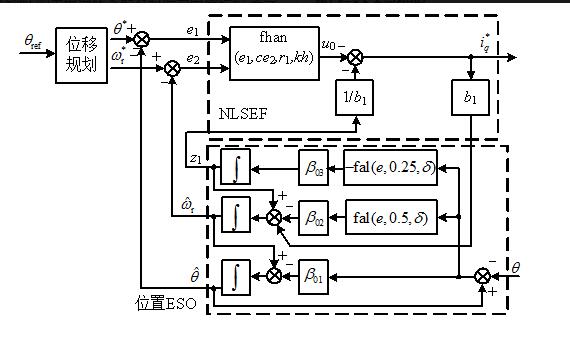
Figure 2 Structure of position and speed composite control
The position and velocity references are generated, and the estimated value of the extended state observer is calculated. After a nonlinear control law, a given value of the q-axis current is obtained.
Therefore, the block diagram of the position and speed control based on nonlinear auto-disturbance rejection is shown in Figure 2. The given position θref is subjected to displacement planning to generate a position and velocity reference, and it is computed with the estimated value of the extended state observer. After a nonlinear control law, a given value of the q-axis current is obtained.
4. Current loop auto disturbance rejection control
In the servo system, when the load torque is disturbed, if the current loop cannot adjust the electromagnetic torque in time, a large deviation will occur in the position, which has a great influence on the performance of the servo system.
Based on the rotor field-oriented vector control, with the id=0 control, the q-axis equation can be expressed as

When the load changes, it will cause the fluctuation of speed ωr, and in formula (10), -ωrψr/Lq change can be regarded as the interference term, and the parameter perturbation of resistance Rs and inductance Lq can also be regarded as the q-axis current loop. Disturbance. Therefore, a first-order ADRC algorithm is used to suppress the disturbance caused by the speed in time so that the influence on the position loop is small. In order to facilitate parameter design and engineering setting, the observer is taken as a second-order linear state observer:
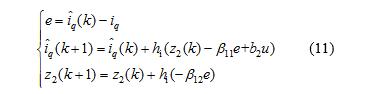
Where: i^q(k)i^q(k) is the estimated value of the q-axis current iq for the kth operation cycle.
K≥0; z2 is the perturbation observation; β11, β12 are the current observer coefficients; hi is the current loop operation cycle.
As mentioned earlier, the performance of ESO has a great influence on disturbance observations. An effective method for selecting linear ESO parameters is to use the concept of bandwidth [20]. The current loop bandwidth is ωi, and the characteristic polynomial of the current loop ESO is s2+ β11s+β12. To better estimate the state and disturbance, let it be the ideal characteristic equation form (s+ωi)2, and then
The number β11 = 2ω and ωiβ12 = ω2iωi2.
The current loop uses linear error feedback rates as follows:
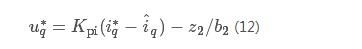
Kpi is the current control gain.
Therefore, the block diagram of the first-order ADRC of the current loop is shown in Figure 3. While observing the current, the extended state observer gives the disturbance quantity z2 of the system, which compensates to improve the system's ability to resist disturbances.
The structure of PMSM double-loop servo drive system based on ADRC control is shown in Figure 4. Using the i* d=0 control mode, the position second-order ADRC controller adjusts the torque current setpoint i* q. The first-order ADRC controller and the excitation current PI regulator of the torque current adjust the corresponding d and q-axis stator voltages. Desired point.
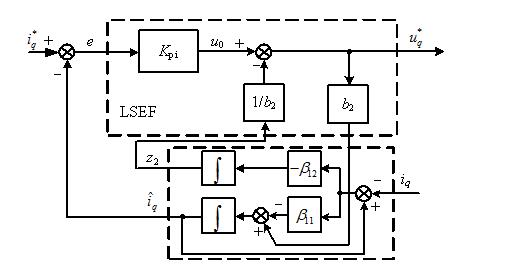
Fig. 3 The first-order ADRC structure of current iq
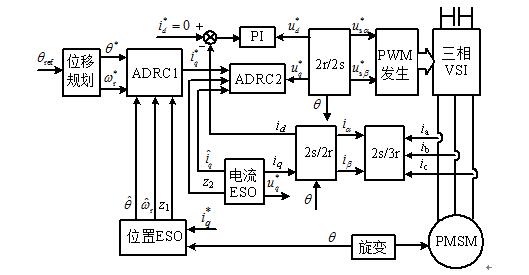
Fig. 4 Control block diagram of dual-loop servo system based on auto-disturbance control
Third, simulation researchThe permanent magnet synchronous motor parameters for simulation and experiment are as follows: rated speed nN=2000r/min; stator resistance Rs=0.212Ω; direct-axis inductance Ld=Lq=3.2mH; moment of inertia J=0.0176kg•m2; pole pair number pn= 4; rotor magnetic flux ψr=0.199T. The DC bus supply voltage is 150V, the current loop control period is 200μs, and the position loop control period is 1ms.
1, expansion of the state observer performance verification
For a given position θref=251.2 rad, the simulation waveforms for position and speed are shown in FIG. 5 . It can be seen that the system can accurately observe the position and rotation speed in the process of steady state and dynamic tracking, indicating that the designed extended state observer has higher observation accuracy.
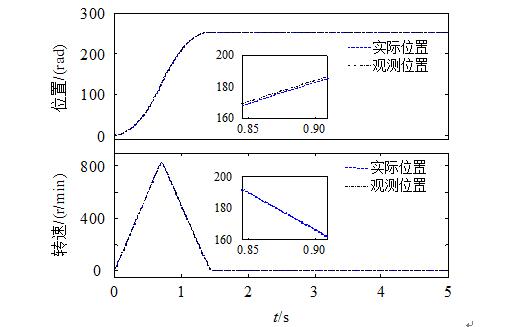
Figure 5 Position and Speed ​​Simulation Waveforms During Positioning
2. Verification of the effect of position loop parameters on control performance
For a given position θref=251.2 rad, the position loop parameter r=3.5, and the simulation waveforms when c is 1 and 6 respectively are shown in FIG. 6 . When c=1, the maximum value is 251.52 rad, the system has an overshoot, and when c=6, there is no overshoot and the response time is shorter. From the zoomed-in waveform, it can be seen that when c is taken, the speed tracking characteristic is 6. Better, verify the theoretical analysis of Section 2.3, show that the introduction of the control parameter c can change the control of the nonlinear feedback control law, by selecting a suitable value can improve the control performance of the system.
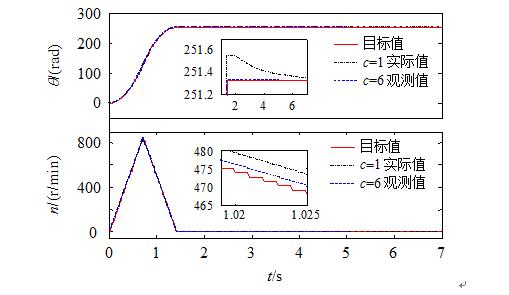
Fig. 6 Position tracking simulation waveforms with different values ​​of parameter c
3, anti-load torque disturbance
The simulated waveform of sudden load during dynamic tracking is shown in Fig. 7. At a given position θref=251.2 rad, a load of 5 N•m is suddenly generated at 1 s, the maximum speed drop is 20 r/min, and the speed is given after 40 ms tracking, and there is no significant fluctuation in the position.

Figure 7 Burst 5N•m Load Simulation Waveform During Dynamic Tracking
The sudden load waveform of the system at steady state is shown in Fig. 8. At 3s, the load of 5N•m is suddenly increased. The maximum speed drop is 18.7r/min, the adjustment time is about 10ms, and there is an error of 0.3rad in steady state. The static and dynamic simulation results show that the system is still stable under sudden load, and it has good rapidity, which verifies that the proposed control algorithm has strong anti-load disturbance capability.

Figure 8 Sudden 5N•m Load Simulation Waveform in Steady State
4. Robustness of the system when the motor parameters are mismatched
In the design of the current loop auto-disturbance rejection controller, the parameter b2 = 1/Lq exists in the observer, so the robustness of the system is verified when there is an error in the inductor Lq. Fig. 9 gives the simulation waveform of the position tracking process when the parameter Lq used in the control is 50% and 200% of the ideal value. The results show that the system is still stable even under the condition of large deviation of the inductance, and the extended state observer can still observe the current iq very well, and it can follow the change of the setpoint value very well, showing a good resistance. The ability to change parameters.
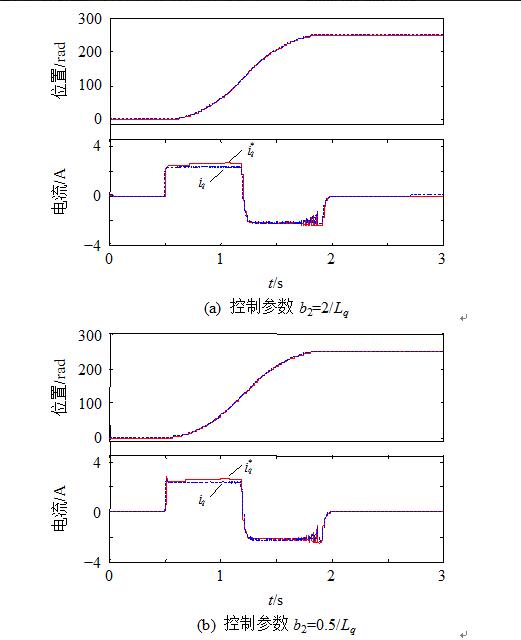
Figure 9 Positioning simulation waveforms when there is an error in Lq parameters
Fourth, the experimental resultsIn order to further verify the proposed control strategy, an experiment was conducted on the dSPACE platform, and experimental data was saved by the matched ControlDesk host computer software.
Figure 10 shows the experimental waveform at a given position θref = 251.2 rad. It can be seen that in the positioning process, both the position and velocity can follow the target value well, and the steady-state error is 0.4 rad.
Figure 11 shows the sudden change in load when the position θref=251.33rad

Figure 10 Position and Velocity Experiment Waveforms During Positioning
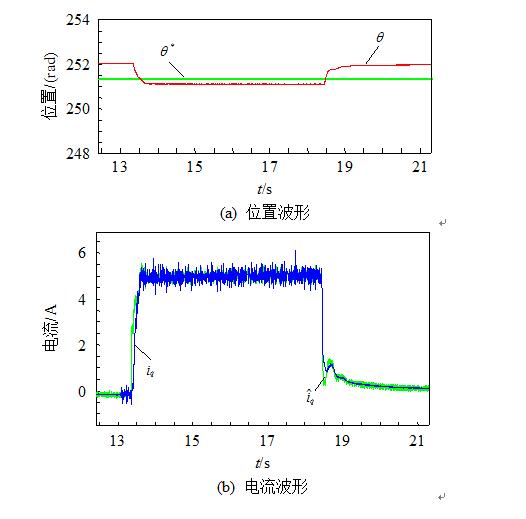
Figure 11 Load mutation experiment waveform
Experiment waveforms. The 5N•m load torque disturbance from the sudden increase of 5s at no load for 13.5s, the error at no-load is about 0.6rad, and the error after loading with 5N•m is 0.2rad. When the mutation at 18.5s is no load, The system is still stable.
Figures 12 and 13 show the experimental waveforms under no-load conditions when the parameters Lq used in the controller are 50% and 200% of the ideal values, respectively. Even if different inductance values ​​are used and the motor parameters are mismatched, the current iq is slightly different, but they all achieve better position tracking effects. At the same time, it can be seen from the figure that when the final steady state is reached,
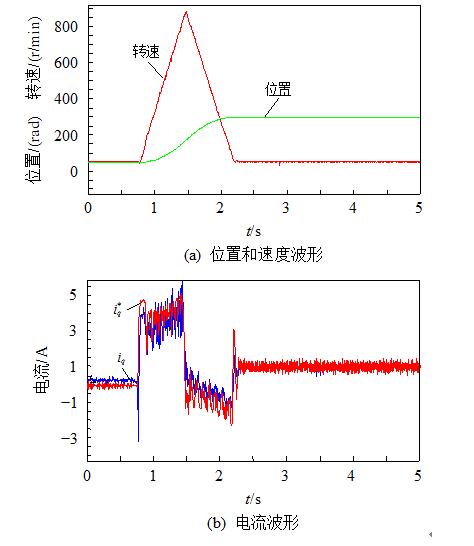
Fig. 12 Control parameter b2 = 2/Lq positioning waveform
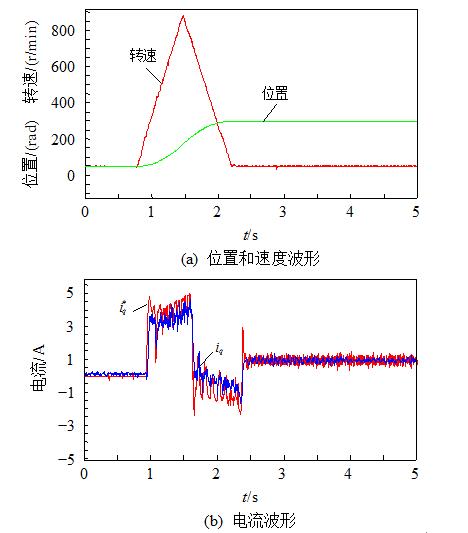
Fig. 13 Control parameter b2 = 0.5/Lq positioning waveform
Iq finally stabilizes at about 1A instead of 0. This is because the motor speed is close to zero at steady state, but the position ESO is still being observed. At this time, since the static adjustment is still in progress, the static friction torque of the motor is not Modeling information is estimated as disturbances outside the ideal model and is compensated to the current loop setpoint i*q, so that iq eventually stabilizes at around 1A.
The above experimental results show that the proposed dual-loop control method based on auto-disturbance rejection control is correct, improves the ability of the system to resist load torque disturbance, and still has strong robustness when the motor parameters are mismatched.
V. ConclusionIn this paper, based on the anti-jamming of the servo system, the ADRC mechanism is proposed to provide a dual-loop auto-disturbance rejection control structure. The second-order nonlinear auto-disturbance rejection controller for position and the first-order linear auto-disturbance rejection control for q-axis current are given. Device design method. Simulation and experimental results show that the proposed position-current double-loop control strategy based on auto-disturbance-rejection control in this paper has a good inhibitory effect on disturbances such as load torque and motor parameter changes, indicating that the control strategy is an effective method. With engineering application value
Ultra-Fast Scanning External Cavity Tunable Laser
Ultra-Fast Scanning External Cavity Tunable Laser,Tunable Diode Laser Analyzer,Applications Tunable Laser,Tunable O-Band Laser
AcePhotonics Co.,Ltd. , https://www.acephotonics.com