Two Methods to Solve the Problem of Unaligned Sequences

Given {1, 2, 3, ,, n}, the full rank is n!, which is the most basic knowledge of high school combinatorics. We use n=4 as an example. All of them are arranged as shown in the following figure (in lexicographic tree format):

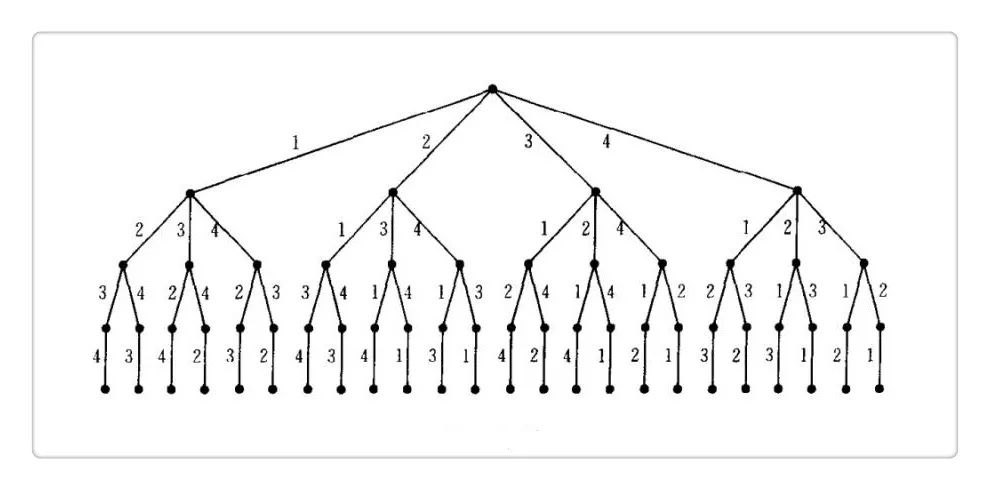
It is easy to think of using recursion to find all its permutations.

Observe the above picture carefully.

Start with 1, followed by the full arrangement of {2, 3, 4};

Start with 2, followed by the full arrangement of {1, 3, 4};

Start with 3, followed by the full arrangement of {1, 2, 4};

Start with 4, followed by the full arrangement of {1, 2, 3}.

code show as below:

/**

*

* author : Limer

* date : 2017-05-31

* mode : C++

*/

# include

# include

Using namespace std ;

Void FullPermutation ( int array [], int left , int right )

{

     If ( left == right )

     {

         For ( int i = 0 ; i < 4 ; i ++ )

             Cout << array [ i ] << " " ;

         Cout << endl ;

     }

     Else

     {

         For ( int i = left ; i <= right ; i ++ )

         {

             Swap ( array [ i ], array [ left ]);

             FullPermutation ( array , left + 1 , right );

             Swap ( array [ i ], array [ left ]);

         }

     }

}

Int main ()

{

     Int array [ 4 ] = { 1 , 2 , 3 , 4 };

     FullPermutation ( array , 0 , 3 );

     Return 0 ;

}

Run as follows:

å’¦~ The recursively written full arrangement is not perfect, it does not strictly follow the lexicographic order. However, a friend who is familiar with C++ certainly knows that there is another simpler and more perfect all-arrangement method.

Defined in the file The two algorithm functions inside:

1, next_permutation, for the current arrangement, if there is a next arrangement in the lexicographic order, return true, and adjust the current arrangement to the next permutation; if not, adjust the current arrangement to be the first in the lexicographic order Arrangement (that is, incremental arrangement) returns false.

2. prev_permutation, for the current arrangement, if there is a previous arrangement in the lexicographic order, return true, and adjust the current arrangement to the previous arrangement; if it does not exist, adjust the current arrangement to the last arrangement in the lexicographic order (that is, descending order), returns false.

/**

*

* author : Limer

* date : 2017-05-31

* mode : C++

*/

# include   

# include   

Using namespace std ;

Void FullPermutation ( int array [])

{

     Do

     {

         For ( int i = 0 ; i < 4 ; i ++ )

             Cout << array [ i ] << " " ;

         Cout << endl ;

     } while ( next_permutation ( array , array + 4 ));

}

Int main ()

{

     Int array [ 4 ] = { 1 , 2 , 3 , 4 };

     FullPermutation ( array );

     Return 0 ;

}

Run screenshots omitted. The output is exactly in lexicographic order.

What did this "wheel" do? (Extracted from Hou Jie's "STL source code analysis")

1, next_permutation, first, look for two adjacent elements from the end of the end, so that the first element is *i, the second element is *ii, and meet *i <*ii, find a set of adjacent elements Afterwards, check from the end of the tail to find the first element larger than *i. Let it be *j, reverse the i, j elements, and then reverse the arrangement of all elements after ii. "Next" permutations and combinations.

2, prev_permutation, first, look for two adjacent elements from the end of the end, so that the first element is *i, the second element is *ii, and meet *i> * ii, find such a set of adjacent elements Afterwards, check from the end of the tail to find the first element less than *i. Let it be *j, reverse the i, j elements, and then reverse the arrangement of all elements after ii. The "previous" permutations and combinations.

code show as below:

bool next_permutation (int * first, int * last)

{

     If ( first == last ) return false ;    // empty interval

     Int * i = first ;

++ i ;

     If ( i == last ) return false ;    // There is only one element

     i = last ;

-- i ;

     For (;;)

     {

         Int * ii = i ;

-- i ;

         If ( * i < * ii )

         {

             Int * j = last ;

             While ( ! ( * i < *-- j ))    // Look forward from the end until you meet an element larger than *i

                 ;

             Swap ( * i , * j );

             Reverse ( ii , last );

             Return true ;

         }

     }

     If ( i == first )    // The current arrangement is the last one in the lexicographic order

     {

         Reverse ( first , last );    // All reversed, ie ascending

         Return false ;

     }

}

bool prev_premutation (int * first, int * last)

{

     If ( first == last ) return false ;    // empty interval

     Int * i = first ;

++ i ;

     If ( i == last ) return false ;    // There is only one element

     i = last ;

-- i ;

     For (;;)

     {

         Int * ii = i ;

-- i ;

         If ( * i > * ii )

         {

             Int * j = last ;

             While ( ! ( * i > *-- j ))    // Look forward from the end until you meet an element larger than *i

                 ;

             Swap ( * i , * j );

             Reverse ( ii , last );

             Return true ;

         }

     }

     If ( i == first )    // The current arrangement is the first one in the lexicographic order

     {

         Reverse ( first , last );    // All reversed, descending

         Return false ;

     }

}

Postscript

This article mainly introduces two methods to solve the problem of the total arrangement of non-repeating sequences: recursion and lexicographic ordering .