In order to obtain a better performance RF receiver front end, filter out various interfering signals in the receiver, and retain the useful signal, the filter must be placed in the appropriate place at the front end of the receiver. In particular, the pre-selected filter placed in the first stage of the system directly affects the noise figure of the RF front end of the entire receiver. By analyzing the noise figure equation of the N-stage cascade system, it is necessary to minimize the loss of the preselected filter and also to have the selectivity required by the system.
1, the choice of pre-selection filterSince the preselected filter is in the first stage of the entire RF front-end system, its performance has a great impact on the entire receiver system. Considering the linearity of the system (avoiding noise caused by nonlinear errors), there should be no preselected filters. Any active device, so the filter should be designed as a passive LC filter [1].
At the same time, for a dedicated short-wave receiver system, the linear phase response (phase shift) is more critical than steep attenuation or amplitude variations, and linear phase shifts and steep amplitude variations are conflicting. Considering their mutual influence and combining the system requirements, the design selected the largest smooth Butterworth bandpass filter with the smallest ripple in the attenuation curve.
2. Design and implementation of preselected filters2.1. Design method of preselected filter
At present, the design method of the analog band-pass filter is to convert the technical specifications of the filter to be designed into a technical index of the analog low-pass filter through a certain frequency transition relationship, and design a low-pass filter transfer according to these technical indicators. The function then becomes the transfer function of the filter to be designed according to the frequency conversion relationship [2].
The four frequency parameters of the analog bandpass filter are Ωsl, Ω1, Ω3, Ωsh, where Ω1 and Ω3 are the lower and upper limits of the bandpass, Ωsl is the upper limit of the lower stopband, and Ωsh is the lower limit of the upper stopband. First, we must normalize them.
Define ΩBW = Ω3 - Ω1 is the bandpass bandwidth, and use this as the reference frequency to normalize the Ω axis, ie
Ηsl = Ωsl / ΩBW, ηsl = Ωsh / ΩBW,
Η1 = Ω1 / ΩBW, η3 = Ω3 / ΩBW.
Redefine Ω 
=Ω1Ω3 is the center frequency of the bandpass, normalized η = η1η3, so that the normalized amplitude-frequency characteristic H(jη) and the normalized low-pass amplitude-frequency characteristic | G(jλ)| can be obtained, and some main correspondences of η and λ can be obtained. Find a point η between η2 - η3 whose corresponding point on the λ axis should be between 0 - λP, since η3 = η /η1, then the corresponding point of η on the η axis should be η /η, and the point at which λ corresponds to the λ axis should be -λ. This can find the conversion relationship between η and λ as
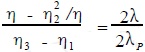(1)
Since η3 -η1 = 1, λP = 1, so there is
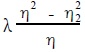(2)
Thereby frequency conversion is achieved. The transfer function G(p) of the filter can be designed using the obtained low-pass filter specifications λP, λs, αP, αs. by
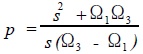(3)
Available
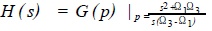(4)
Thus, the required transfer function of the bandpass filter can be found.
Through the above method, the design of the Butterworth analog bandpass filter can be converted into the design of Butterworth analog low-pass filter [3]. Note that after the N-stage low-pass filter is switched to bandpass, the order becomes 2N.
Given the technical indicators αp, Ωp, αs, Ωs of the analog low-pass filter, where αp is the maximum attenuation allowed in the passband, αs is the minimum attenuation that should be achieved in the stopband, and the unit of αp and αs is dB, and Ωp is the pass. With the upper limit angular frequency, Ωs is the stop band lower angle frequency [4].
Αp, αs are all functions of Ω, their size depends on the shape of |G(jΩ)|, for which purpose an attenuation function α(Ω) is defined, ie
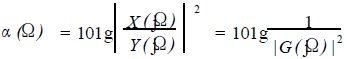
(5)
Thus, equation (5) relates the four specifications of the low-pass analog filter to the squared characteristics of the filter.
Because of the large difference in the frequency range of each filter. In order to normalize the design, the frequency parameters of the filter need to be normalized. Let the given actual frequency be Ω (or f), and the normalized frequency be λ, for the low-pass filter,
λ = Ω / Ωp (6)
Let the normalized complex variable be p, p = jλ, obviously
p = jλ = jΩ /Ωp = s /Ωp(7)
The design of the Butterworth low-pass analog filter can be performed in the following three steps.
1) Normalize the actual frequency Ω
Normalized squared characteristic
(8)
It can be seen that there are only two parameters C and N in |G(jλ)|2 (or |G(jΩ |2), and N is the order of the filter.
2) Find C and N
From (5)
α(λ)= 101g(1 + C2λ2N), (9)
Formula,
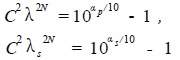(10)
Because λp = 1, so
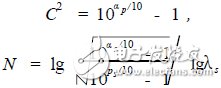
(11)
This way C and N can be obtained.
If αp = 3 dB, then C = 1, so the Butterworth low-pass analog filter design has only one parameter N left.
3) Determine G(s)
Because p = jλ, there is
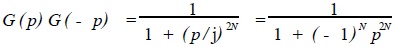(12)
By 1 +(-1)Np2N = 0
Solutions have to
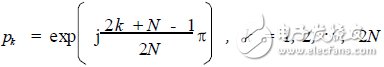
(13)
Thus, the 2N poles of G(p)G(-p) are equally divided on a circle having a radius of one on the s plane, and the distance is (Ï€/N) rad.
In order to ensure that the designed filter is stable, the pole of the left plane should be given G(p), ie
(14)
such
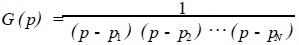(15)
If N is even, the poles of G(p) are conjugated, ie
Pk,pN +1 - k,1 ≤ k ≤N /2 (16)
This pair of conjugate poles constitutes a second-order system, ie
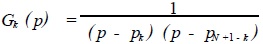(17)
The total transfer function should be a cascade of N /2 type second-order systems, ie
, N is an even number. (18)
If N is odd, it will be cascaded by one system and (N - 1)/2 second-order systems, ie
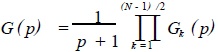
, N is an odd number. (19)
Thus, the normalized transfer function G(p) is obtained. Using the relationship of equation (7), the actual required G(s) is obtained.
In order to realize the transfer function G(s) of the two-port trapezoid, the focus is on finding z11 and z22 using G(s), and then implementing z11 and z22. The zero of the transfer function coincides with the zero of z21, so it is not necessary to find z21.
The basic idea of ​​deriving z21 and z22 is that the average power of the input LC network should be equal to the average power of the LC network output. To this end, define the auxiliary rational functions K(s) and K(ω2) so that
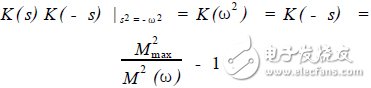
(20)
Where: M(ω)= |H(jω)| is the amplitude-frequency response, and Mm ax(ω)= is the maximum value of the amplitude-frequency response. K(ω2) is an even rational function of ω, and K(- s2) is an even rational function with respect to s with real coefficients, and
K(ω2)≥ 0(21)
The complex zero of K(- s2) appears in quadrant symmetry, ie, s1 = σ1 + jω1, s2 = σ1 - jω1, s3 = 2σ1 + jω1, s4 = -σ1 - jω1, and σ1 and ω1 are positive real numbers. Since K(s) is a rational function with real coefficients, a complex conjugate zero pair must be selected from the left or right half of the s complex plane.
The real zeros of K(- s2) appear in pairs, ie s1 = σ1, s2 = -σ1. Just select a zero for K(s).
The Hn(s) used to find the two-port ladder implementation is
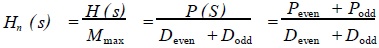(twenty two)
Where: Deven is an even polynomial about s, and Dodd is an odd polynomial about s. P(s) is determined by the zero of the transfer function, Peven is the even polynomial for s, and Podd is the odd polynomial for s.
Can be obtained from equation (22)
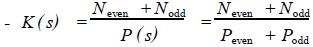(twenty three)
Where: Neven is an even polynomial about s, and Nodd is an odd polynomial about s. The pole of K(s) is used as the zero point of the transfer function.
As can be seen
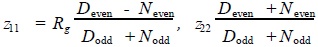
The impedance z11 can be achieved by the classical Foster method.
According to the above method, the Butterworth bandpass analog filter required by the system can be realized. The system designed is simulated by ADS, as shown in Figure 1.
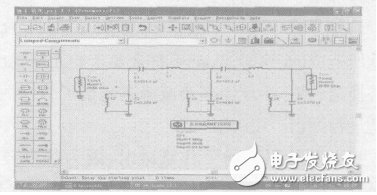
Figure 1. Simulating an LC filter with ADS
The simulation results are shown in Figure 2.
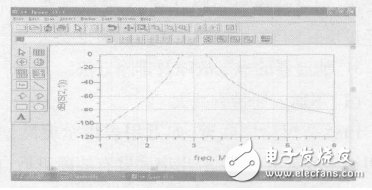
Figure 2. LC filter frequency response simulation results
2.2. Implementation of preselection filter
2.2.1, the production of inductive components
Through the above analysis, the LC filter that meets the requirements can be designed, but the implementation of the filter has certain difficulties. The implementation of the filter is mainly to achieve high precision, high Q value, high self-resonant frequency and inductance with small parasitic parameters. Generally speaking, for an inductor with a small inductance value, an enameled wire is directly wound into an air-core coil [5].
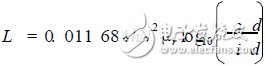
(twenty four)
Where: L is the inductance value; h is the thickness of the magnetic ring; od is the outer diameter of the magnetic ring; I d is the inner diameter of the magnetic ring; μr is the magnetic coefficient of the magnetic ring; N is the number of coils.
After winding, select a capacitor of about 50 pF and connect it in series. According to the principle of LC oscillator circuit, the parallel resonance point is measured by vector network analyzer. The exact value of L can be obtained by the conversion relationship between LC and the resonant frequency.
2.2.2, adjustment of pre-selection filter
After the filter assembly is completed, it is necessary to measure various electrical characteristics. If some of the performance does not meet the technical requirements, adjustments are made until the technical requirements are met.
The adjustment process is as follows:
1) Tuning on the printed board, the resonant circuit and other components are disconnected, and the leads should be as short as possible for accurate tuning.
2) After the tuning is completed, the points are connected to form a filter. First measure the reflection attenuation of the pass band. If the tuned resonant frequency has shifted a large amount, recheck and adjust the resonant frequency. If the reflection attenuation is only slightly below the required value at a single point, the attenuation peak frequency can be fine-tuned to meet the requirements.
3) If the passband attenuation is too large, one reason is caused by the original Q value being too low. At this time, find and replace the components that do not meet the requirements; another reason is that the attenuation peak frequency is biased, and then re-tune.
4) When measuring the operational attenuation of the stop band, because the frequency is high, if a filter with a high stop band is encountered, sometimes the individual points will not meet the requirements. At this time, the attenuation peak frequency can be fine-tuned so that the entire stopband characteristics meet the requirements. However, after the attenuation peak frequency is adjusted, the passband characteristics are affected. It needs to be adjusted repeatedly to make both meet the requirements at the same time.
2.2.3, common faults and troubleshooting methods of filters
(1) Unreachable or passband attenuation
1) Short circuit the series arm by section. If the multimeter indicates a sudden increase, it indicates that the series arm is faulty. After detecting that the series arm is faulty, check which components in the section have failed according to the above method.
2) If the series arm has not been faulted after inspection, check the parallel arm again. When checking, disconnect the parallel arm one by one, find out that there is a fault in the parallel arm of a certain section, and then use the same method to check whether the component of the section is faulty.
3) The attenuation of the high-frequency end of the passband is increased, and the attenuation peak frequency and resonance attenuation of the upper stopband can be measured. The attenuation at the low frequency end is increased, and the attenuation peak frequency and resonance attenuation of the stop band can be measured.
(2) Large attenuation fluctuations in the passband
1) Check the resonant frequency of the series arm and the parallel arm separately.
2) Check the insulation resistance of the capacitor.
3) Re-tune or replace components.
(3) the stopband attenuation decreases
1) The Q value of the parallel arm element drops. Measure the Q value of the inductor and capacitor.
2) The parallel arm resonance frequency is offset. Measure the resonant frequency.
3) The ground terminal is not in good contact. Check with a multimeter.
(4) Increased nonlinear distortion
1) The magnetic core is subjected to shock displacement, which changes the air gap of the magnetic circuit, causing magnetic saturation and increasing harmonics. The resonant frequency of the circuit can be measured separately with high and low levels. If the resonant frequency changes with the level, it indicates that the magnetic core has magnetic saturation and should be replaced.
2) The contact of the capacitor element is poor, and the active resistor is formed by the dummy solder, causing the harmonic to increase. The contact resistance of the capacitor can be tested with an impedance bridge, and the contact resistance of the original connector can be checked with a multimeter.
(5) Balanced attenuation of the balanced filter decreases
1) The series arm components are variable or poorly insulated from the ground, causing up and down asymmetry. The balance attenuation should be measured section by section to determine where the fault is.
2) The parallel arm has a short circuit to ground. The degree of insulation of the parallel arm components to ground should be checked.
(6) Impedance characteristics are not good (reflection attenuation is too small)
1) Check the resonant frequency of the series arm and the parallel arm separately.
2) Check for component values.
3, the conclusionIn short, dedicated short-wave receivers are increasingly moving toward high performance and high integration in design and implementation. In terms of performance, the receiver is mainly developed in terms of high linearity, large dynamic range, high sensitivity, and high resolution. The most important thing to achieve these goals is to achieve a filter with excellent receiver performance. According to this requirement, this paper analyzes and implements a preselected filter that meets the requirements of the RF short-end system of the dedicated short-wave receiver from the perspective of theoretical algorithms.
Diesel Gensets,Generator Electric,Generador Electrico,Generator Electric Start
Wuxi Doton Power , http://www.dotonpower.com